在AB测试中，对照组和实验组的样本量越大，实验时间越长，这是常识性的判断，但实际上是由统计显著性决定的。
统计显著性的意思是，对照组和实验组的数据差异也许是真实存在的，而不是随机误差。周期越久、样本量更多的AB测试会更加有说服力，在实际工作中，产品或活动的迭代速度十分迅速，要求AB测试的实验周期要尽量控制，测试前对样本规模进行预估十分重要。
在计算完预估的样本数量之后，还有一个重要工作就是预估实验周期。
如果可靠的AB测试中，每组实验需要2900个样本量，但产品每天只有200的日活用户，分成两组后每组是100用户，则意味实验需要29天后才可达到需要的样本量，这个时候就要评估此周期是否可接受，周期过长，说明这个AB测试在现阶段进行是不合适的。
一. 测试结果分析
样本规模预估是在AB测试前进行，因为优化的转化数据是预估的，样本量和实验周期都是预估数据，帮助我们在AB测试前对测试样本和周期有个初步判断。
在实际的AB测试实验结束后，还需要对实际的结果数据进行统计显著性检验，保证对照组和实验组的数据差异是可信的。
当我们输入AB数据时就可以看到转化率的差异，和试验结果的统计显著性结果。
以上图为例，B组的转化率比A组高，但因为样本量较小，试验结果没有达到显著的统计学差异，所以我们不能得出B组优化比A组更好的结论。这个时候有两种选择，一是继续实验，积累更多的实验数据后进行分析，二是放弃实验，得出此次优化没有明显提升的结论。
但不是继续实验一定会得出显著性差异，如果样本量继续增大，但是转化率差异减小，就意味着需要更多的样本量，这种情况往往说明两个版本的差异确实不大，但是也需要根据实际情况判断是否需要停止AB测试。
二. 反向相关指标
在进行AB测试时，一般情况下会有一个核心指标来判断实验结果，同时会有一些支持或辅助指标来更好地监测实验和分析结果。但是不能忽略的是一些反向指标，反向指标就是AB测试实验中可能会负面影响的指标。
新用户首单转化率在这个实验中就是一个值得关注的反向指标。AB测试为了实验的速度和效果，往往会关注少部分关键流程节点和核心指标，但是忽略反向指标，却有得不偿失的风险。
三. 辛普森悖论
某些条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论。
四. 分层实验
将多个实验建立起分层结构，每一层实验使用过的流量，下一层的实验可以继续用。
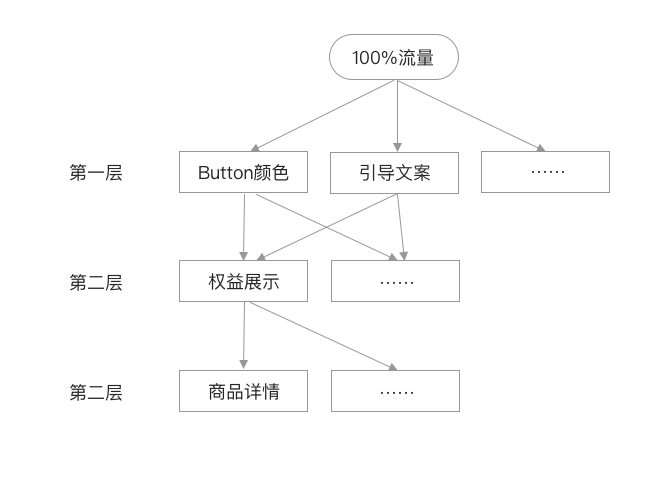
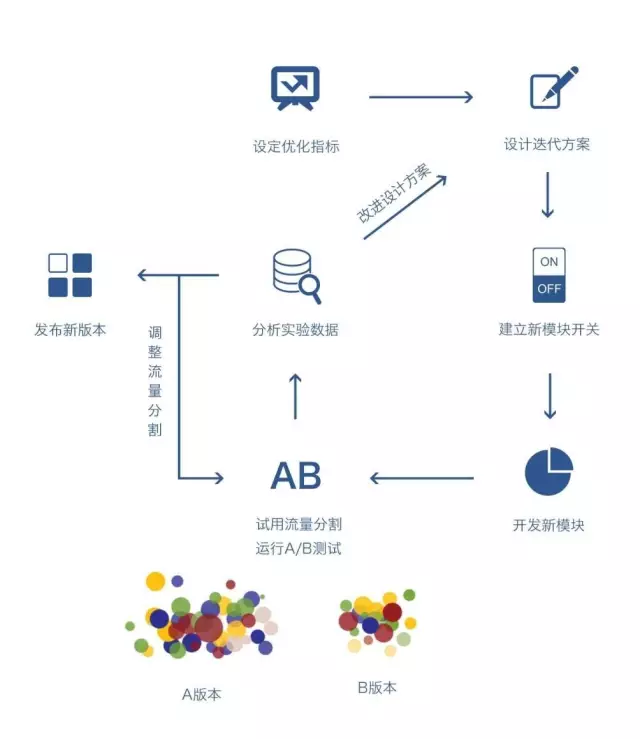
以电商产品的新人流程为例：
新用户下载打开APP后，首页有新人礼包的入口，点击进入后可以查看新人权益和优惠商品，新用户查看新人商品后完成下单，这就是新用户转化的基本路径。为了优化现有的新人转化流程，从新人礼包的首页展示、落地页展示、新人商品详情页同时进行了多个AB实验。
在首页展示上，同时进行了按钮颜色和引导文案的AB实验，为了保证变量的唯一性，按钮颜色实验中，包括文案等其他内容完全是一致的，文案实验中，包括按钮颜色等其他内容也是完全一致的。这就需要把100%的流量分成2部分，假设为各50%，即50%用户进行按钮颜色实验，其余50%用户进行文案实验。
进入到新人页面之后，对权益展示的方式又进行了AB实验，从首页来的流量都进行权益展示的AB实验，来自第一层100%的流量刚进行了按钮颜色和文案的实验，为了避免上层实验对权益展示实验的影响，从上层来的流量要随机分配到权益展示实验的AB两组，这就是分层实验中的流量正交，均匀分配上层流量。
各团队间也要保持沟通，避免单打独斗进行实验，却不知被对方的实验影响了结果，得出不恰当的结论。
